Would you trust a self-driving car to take you on your next journey? If not, why not? Is it because you don’t know what decisions the car is going to make along the journey to keep you safe?
This question, specifically, how do you ensure the safety of a system if you don’t know what the system itself is doing, doesn’t just relate to self-driving cars though. It could be asked about other complex systems, especially those utilising Artificial Intelligence (AI) and machine learning (ML) techniques.
Over the past few years, Think have delivered several analytical projects that have supported safety assurance activities of complex systems. From these projects we have developed an expertise on ways to approach to safety assurance of different systems and more importantly have started to consider what to do when system complexity increases and you don’t know what the system itself is doing.
We’ll go into this further but to start we’ll take a look at the very basics of safety. Then we will progress to look at the challenges of “simple” and “complex” system safety assurance, touch upon the possible safety implications of the future of Deep Neural Networks (a.k.a. Deep learning) and ask some thought provoking questions about where it is heading.
What do we mean by Safety?
Whilst safety is a relatively simple term to think about, it is more challenging to measure. The word can be used to describe the state of security (or lack thereof) of pretty much anything – people, animals or money to name a few. In aviation, we tend to stick with the ICAO definition: “The state in which risks associated with aviation activities, related to, or in direct support of the operation of aircraft, are reduced and controlled to an acceptable level.”
To quantify safety, we need to think of the severity of a certain outcome as well as how frequently it is expected to occur. This is known as risk. Severity is usually characterised subjectively. Probability, however, can be estimated using a variety of measures. Safety is not binary. Any operation/system can never be 100% risk free. The world is extremely complicated and in every macroscopic situation there are many variables to consider. Different outcomes have different risk factors and there are varying chances of each occurring. Safety science and risk analysis try to answer the question: Is this level of risk acceptable?
Safety assurance of “Simple” Systems
I am defining a simple system here as one where a selection of inputs can be used to generate a set of outputs using a known and defined set of processes. A good way of thinking about it is that if a human could (given time) follow the same steps and arrive at the same outputs, it is “simple”.
Assuring the safety of simple systems can be achieved with a variety of methods:
- Do we need to estimate the direct effects of the system implementation itself in controlled scenarios? Fantastic. Generate simulated data with Monte Carlo simulations.
- What if we already have some historic data deemed relevant enough to use for system testing? Brilliant, we can build a model to replicate the system performance and measure the outcomes.
A bit of data manipulation, process implementation and statistical analysis, and hey presto you’ve got your answers. Measure these against your performance requirements and you’re good to deliver your verdict.
The main challenge though is input parameter selection. There are often a seemingly infinite set of input parameter combinations, and there is often no incentive or time to test every possible combination.
An interesting mathematical example that mirrors this issue is the “Four colour theorem”. The proposed theorem, in simplistic terms, states that to divide a “map” into any number of coloured regions where each region has no adjacent region (shares a boundary with) of a shared colour, only 4 colours are ever required. The states of the USA are represented as such below:
©HaseHoch2 – stock.adobe.com
Proving this by hand requires checking every possible map configuration, of which there are an infinite amount, by inspection. This of course is impossible. The methods employed lead to the computer originally reducing this infinite number of maps to a more manageable 1,834 (which since has been reduced further) which were all verified by computer AND by hand. The method of “reduction” here is practically impossible to reproduce by hand – and hence where the disputes lie. But, being verified by many different implementations, leads most to agree its validity.
Unfortunately, there isn’t ever time to test all possible combinations of input parameters and we’d be lucky to find a mathematical method of narrowing them down like this, but in contrast, despite the rigorousness required for a safety case it is never expected to be proved in every single case like a mathematical proof. The point being made here is a finite number of testing configurations is always enough.
We need to be able to select the appropriate inputs that are believed to be representative of important scenarios for the system. Choosing the correct input data tends to require operational experience and hence human subjectivity. There is, however, always a risk that upon deployment the system fails when dealing with a situation not considered. In a “simple” system, we can usually be satisfied with a safety assessment with enough relevant testing configurations, if the process can be validated and verified. After all, to assess a system, we need to be able to see what it is doing, don’t we?
Safety assurance of “Complex” systems
This begs the question: what if we don’t know what the system itself is doing? This may seem a bizarre concept for some; but with the rise of Artificial Intelligence (AI), machine learning techniques and real time manipulation of huge datasets we’ve hit a period where we can develop tools and systems that can “learn”, rather than simply following the commands of a pre-determined algorithm. I am defining a system with these properties “complex”.
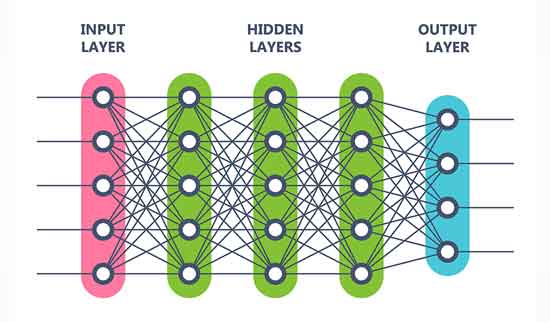
©Dmitrii Korolev – stock.adobe.com
This diagram shows the typical layout of a Deep Neural Network (DNN) – a machine learning tool developed that somewhat mimics the neural connections of our own brains (albeit much simpler now!). The “Hidden Layers” here represent the processing the DNN performs, and the clue being in the name, are unknown to us. Worse still, other than by observation of the outputs, we don’t know how the system will respond to different inputs. All we can get from this are the system outputs based on a set of inputs. Can we justify a system’s safety with just this?
The truth is it depends who you ask. Many people believe that if it is impossible for a human to check by hand, then outputs cannot be verified. In a simple system as mentioned, we know the process. A human could take the inputs and use the defined process to calculate the outputs and then compare to the outputs of the system. There is no way to do that without knowing the process!
The “Four-Color Theorem” strikes some parallels with a non-simple system such as this, namely the map reduction protocol. Although technically fully defined, it is practically impossible to perform this procedure by hand and yet, most of the mathematics community accepts its results. Attitudes on machine learning are rather similar in this regard; there is less emphasis on the process verification and more on the result validation. Ultimately, the results must be accurate and often we assume the model is doing what we want it to do, although model verification is of course still important.
Input choice becomes even more important with machine learning models. The very nature of the model is defined by the data that is used to create it; and as such there is always a risk of using training data that doesn’t capture everything required (causing underfitting) or using test inputs too reminiscent of the training sets (causing overfitting).
Machine Learning engineers need to find the training set (or selection of training sets) that gives an average accuracy acceptable across a wide range of testing situations, again usually decided amongst operational experts. Sometimes data quantity and variety can be a blocker for this – it is unlikely there will be available data representing every scenario required. Is it acceptable to use simulated data to increase the variety of input data? How can we be confident enough to combine this with “real” data?
Often Machine learning models are tuned with the aid of “hyper-parameters”, essentially configuration parameters that control “how” the machine learns. In contrast, these are controlled by humans, whereas the standard model parameters are determined by the machine. This can introduce an extra dimension to model building and validation. A common example would be the learning rate in the gradient descent algorithm. In recent years, however, methods to automate optimal selection of these hyper-parameters have been developed – and I expect this field to continue growing in the future.
Adaptive DNNs
What are the future implications of this area of technology? Our industry, like many others are now, is beginning to use tools that have “adaptive” learning models, namely those that feed in new data and re-train in real time. An example elsewhere is networks powering self-driving cars; these require real time evolution to improve their performance and are slowly getting safer over time.
Adaptive models present new difficulties. Namely, after the initial training of the model with the input selection as described above, further “training sets” when the system goes live are not chosen but are provided as real data given in real time. It would be thought that the very nature of an encompassing initial training input selection should be robust enough to capture all possible real-life scenarios, but as all future data provided will further affect the model, the accuracy of the model will very much vary over time.
In these situations, time now becomes an important factor. Ideally, an adaptive model will maintain a consistently high accuracy continuously across its deployment cycle and not just across a variety of static datasets. How can we be sure that this is the case? If the model is learning during deployment, we are assuming it is doing so correctly.
One thing is for certain: accuracy during real time deployment will be heavily affected by the pre-deployment training inputs. A model’s success in real time will help to indicate if initial training material was sufficient. This leads me to believe that deployment simulations for systems like these will need to be more rigorous than ever; and we will have to come to accept that with systems like these we will never know the true extent of how well it performs at a given time. In an industry like aviation, where safety is so critical, what will be required of the safety assurance process to allow these systems to become commonplace in the industry?
Verification of adaptive models also becomes more complicated, as models will change based on the time, order and chosen hyperparameters. Other issues arise from the format of live input data too, as models can trip up on incorrectly formatted inputs. We won’t go into these here, but it does raise more difficult questions.
Conclusions
The “4 colour theorem” example can teach us something: Although it may be operationally unrealistic to test all possible configuration scenarios in a complex system, if a high level of accuracy can be maintained across a wide enough range of situations then this should suffice. The more complex the system, in particular branching into machine learning technologies, the more taxing result validation becomes, and more of a focus it requires in contrast to result verification. The future of this technology will come with a myriad of new safety assurance challenges, but it is an interesting future for the industry, nonetheless.

Author: George Clark, ATM Consultant


Recent Comments